3.6 解偏微分法(Partial Differential Equations Method)

 

    給定初始值於選定之偏微分方程式，而求出初猜點。 再代入這些點，求出邊界值，然後再用內插或外差法求其邊界內的點，繼續重複這些動作直到收斂。

 

    其求解的方法依不同的邊界條件情況分為解橢圓型(Elliptic)、拋物線型(Parabolic)與雙曲線型(Hyperbolic)三種方法。 以偏微分方程求解一區域內部之邊界值問題時，若邊界式完全封閉的，其偏微分方程式必為橢圓型偏微分方程式(Elliptic Equation)，否則即是拋物線型偏微分方程式(Parabolic)或雙曲線型偏微分方程式(Hyperbolic)方程式。

 

    於卡式座標系中，最簡單的橢圓型方程式之格點座標的轉換即是以下的拉氏方程式(Laplace Equation):

                                               (3-25)

 

    由於以循環收斂方式求解橢圓型偏微分方程式時，致使內部格點呈均勻分佈，而有導致格線分佈於凹型邊界(Concave Boundary)附近稀疏、凸型邊界(Convex Boundary)附近密集的特性，不易控制網格的分佈。 將圖2-2(c)的O-Type網格經解橢圓型偏微分法計算後之結果如圖3.24所示。

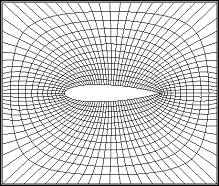
圖3.24 解橢圓形偏微分法的O-Type網格

 

    為了控制內部區域的格點分佈，加入控制參數之後，即成為以下的Poisson Equation:

                                        (3-26)

其中, ,  為控制方程式。

置換式中的, 及後

   

       (3-27)

   

其中

   

    是矩陣中位於元素的cofactor

                                               (3-28)

                                        (3-29)

而其中為賈氏轉換(Jacobian Transformation)，

                                                 (3-30)

 

    解偏微分法雖然具有網格線平滑、傾向正交且絕不會重疊的優點，但由於需經過疊代的過程，因此有速度慢、不易控制點分佈的缺點。

 

    由於代數法與解偏微分法各有其利弊，因此以代數法作格點分佈預測，得到一組符合需求的粗糙網格後，再經由解偏微分法作循環計算來平滑網格的分佈，是較合實際的方法。

 

    值得注意的，代數法中多方向內插網格點法(Transfinite Interpolation)與解偏微分法中之解橢圓形方程式格點法由於在近十年來發展成熟，已成為現今結構性網格點生成法之主流。 然而解拋物線型方程式格點法與解雙曲線型方程式格點法，由於強調簡單的格點預測和具有求解速度快的優點，雖技術尚未完全成熟，但未來的發展不容忽視。